משפחת המרובעים

משפחת המרובעים היא משפחה של תצורות גאומטריות בעלות ארבע צלעות ו360 מעלות
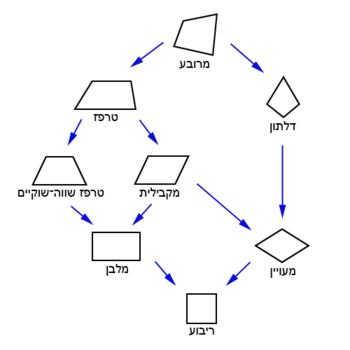
ישנן 6 תצורות בסיסיות של מרובעים: דלתון ,מקבילית, מעוין, מלבן, ריבוע וטרפז
ועליהן נדבר בהרחבה בספר.

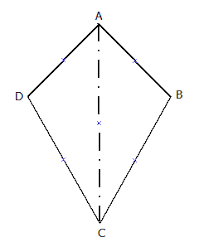
דלתון

הגדרה:

שני משולשים שווי – שוקיים בעלי בסיס משותף

תכונות:

1. בדלתון ישנן 2 זוגות של צלעות סמוכות ושוות.
2. בדלתון ואלכסונים מאונכים זה לזה.
3. בדלתון האלכסון הראשי הוא חוצה זוויות.
4. בדלתון האלכסון הראשי הוא תיכון לאלכסון המשני.

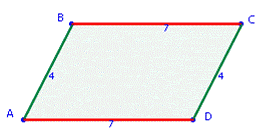
המקבילית

הגדרה

מרובע בו כל זוג צלעות נגדיות מגבילות

תכונות

1.במקבילית כל זוג צלעות נגדיות מקבילות זו לזו

2.במקבילית כל זוג צלעות נגדיות שוות

3.במקיבלית כל סכום צלעות במוכות.180

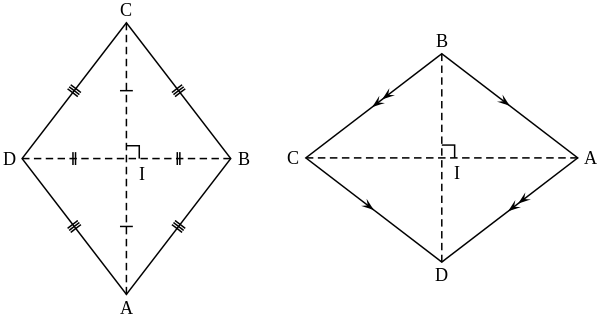
מעוין

הגדרה

מעוין הוא מרובע שהוא מקרה פרטי של דלתון ושל מקבילית בו כל הצלעות שוות באורכן

תכונות

1במעוין כל הצלעות שוות

2במעוין כל צלעות נגדיות מקבילות

3במעוין כל זוג זוויות נגדיות שוות

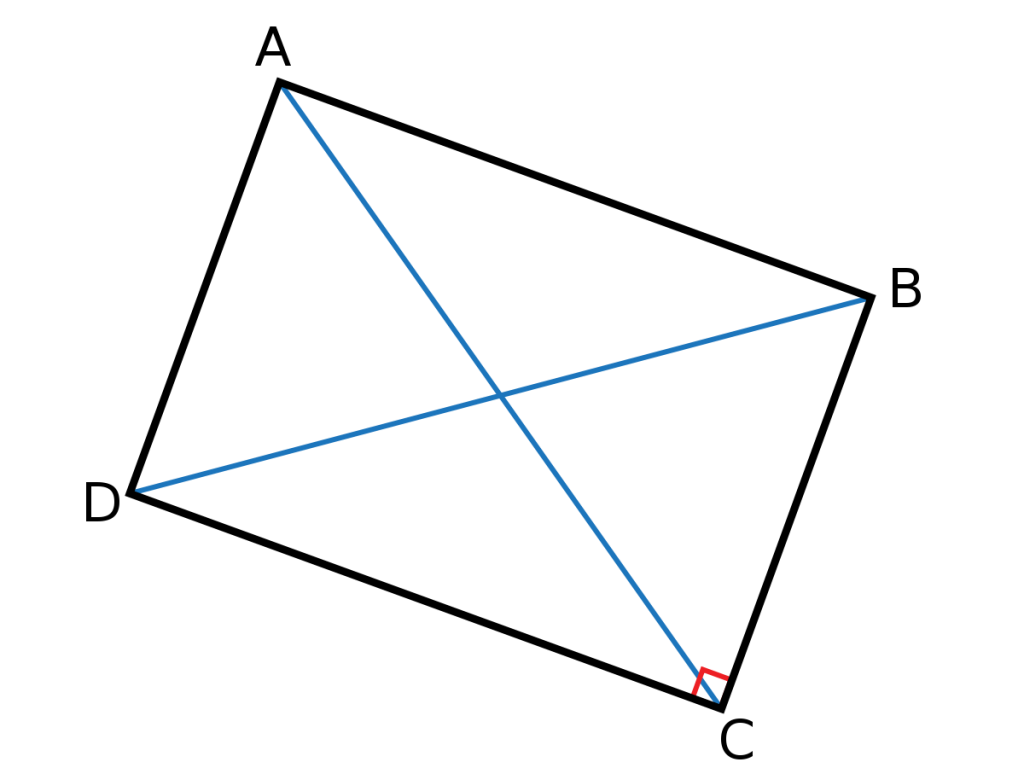
מלבן

הגדרה

מלבן הוא מרובע שהוא מקרה פרטי של מקבילית כלומר מקבילת ישרת זווית

תכונות

1במלבן כל זוג זוויות נגדיות שוות

2במלבן כל זווית היא ישרה

3במלבן הלכסונים זה את זה

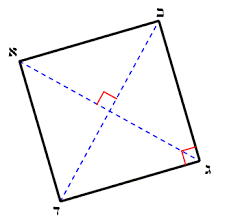
ריבוע

הגדרה

ריבוע הוא מרובע שהוא מקרה פרטי של מעוין ישר זווית או מקרה פרטי של מלבן שווה שוקים

תכונות

1בריבוע כל זוג צלעות נגדיות מקבילות זו לזו

2בריבוע כל הצלעות שוות

3בריבוע הלכסונים חוצים זה את זה

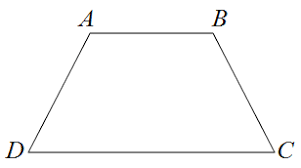
טרפז

הגדרה

טרפז הוא מרובע בעל זוג אחד של צלעות מקבילות

תכונות

1שני בסיסים מקבילים אחד לשני

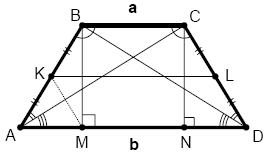
טרפז שווה שוקים

הגדרה

טרפז הוא מרובע בעל זוג אחד של צלעות מקבילות

תכונה

1 שני בסיסים מקבילים אחד לשני

2זוג צלעות נגדיות בעלות זווית בסיס שונה